UUIDs - Mess Within a Widely Used Standard
Written on . Posted in Database.
UUIDs - Mess Within a Widely Used Standard
It's time to dive into the wild, wacky, and sometimes downright infuriating world of UUIDs. Yes, those strings of alphanumeric chaos that we love to hate and hate to love We're not here to explain what UUIDs are (Google that if you must), but rather to vent, rant, and explore some wild ideas about how V7 can help in some ways, specially with S3s (S3s requires a separate rant of its own)
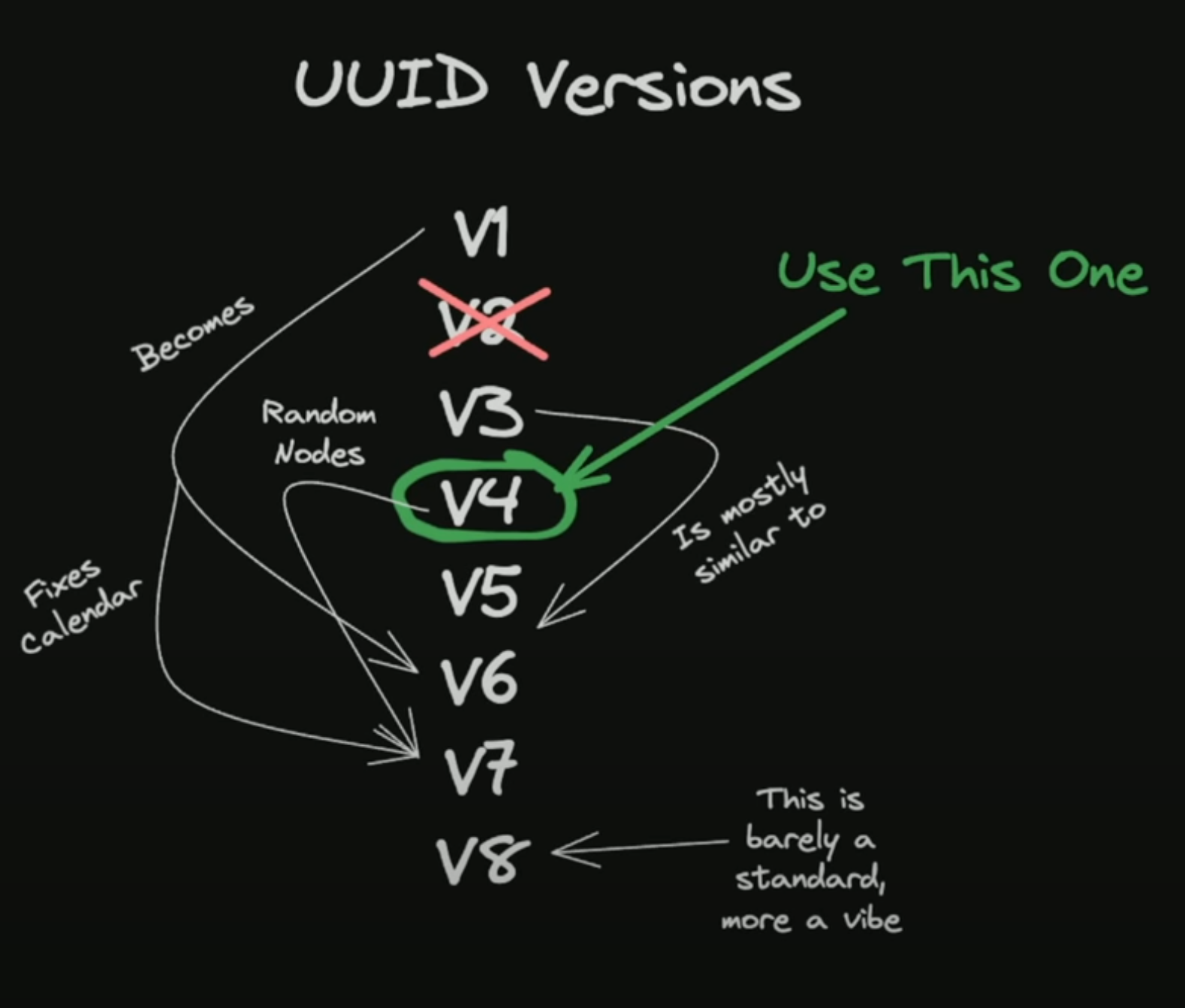
A quick overview of what a mess of versions it is!
I like this illustration from @t3dotgg and this post The Problem with Using a UUID Primary Key in MySQL will give you a very good explanation of how messed up this is, which basically translates to,
UUIDv1 - Uses the Gregorian calendar 🤷♂️ segments looks like ['time_low'-'time_mid'-'time_low_and_version'-'clock_seq_and_version'-'node'] now using the Gregorian calendar is not the biggest issues here, rather they had the biggest segment set to 'node' which is the unique address of the system generating the UUID. I'm no security expert but this looks bad
UUIDv2 - nothing interesting here, they replaced the 'low_time' component of the UUID with POSIX user ID
UUIDv3 and v5 - they started using a 128bit hash and both versions use a different hash MD5 and SHA1 respectively, the interesting part here is that V3 and V5 are similar but not V4, and V4 is what is widely used
UUIDv4 - this is what most of the population uses for their random keys and in my opinion, this is the simplest of them all, it just uses a set of random alphanumerics, with the exception that the first position of the 3rd segment is always set to the version number (seen throughout the versions)
UUIDv6 - now V6 is very similar to V1 flipping the timestamps, meaning the most significant portions of the timestamp are stored first. now, in turn, this makes it a little more sortable, since the most significant portion of the timestamp is upfront
UUIDv7 - now this is the only version I can think of using in some cases instead of V4, this basically finally uses the UNIX timestamp instead of the Gregorian calendar and the rest of the string is just random alphanumerics, which makes it less trackable back to their source and this is what we will discuss moving forward
UUIDv8 - this permits vendor-specific implementations while adhering to RFC standards and the illustration says its more of a vibe than a standard now
UUIDv7 and Simple Storage Solutions (or databases in general)
Moving forward we will mostly discuss databases, optimizations through the tree structure used in modern databases and a lot of what I thought through the week (might be very dumb), so read the related papers mentioned below to get a better understanding of things.
Trees 101
Now Trees, with their hierarchical structure, play a pivotal role in all of computer science in my opinion also providing a backbone for storing indices for huge databases, (If you don't know about Trees consider taking one of the MITOCW courses on data structures), for now, we will talk about B-Trees often called as balanced trees but it's not known that what B stands for in the B-Trees, also we'll talk about B+ Trees which is a much more widely accepted data structure when storing huge amounts of data
B Trees
Assuming you know about BSTs, we'll work with a modification that considers that now every node can store two keys, now you have 3 paths to take when searching for a key very similar to what you would do for a binary search tree, now to formalize this, each node in a B-Tree of order 𝑑 contains at most 2𝑑 keys and 2𝑑+1 pointers as shown below, now the keys can vary from node to node, but each must have at least 𝑑 keys and 𝑑+1 pointers, such that every node is at least half full.
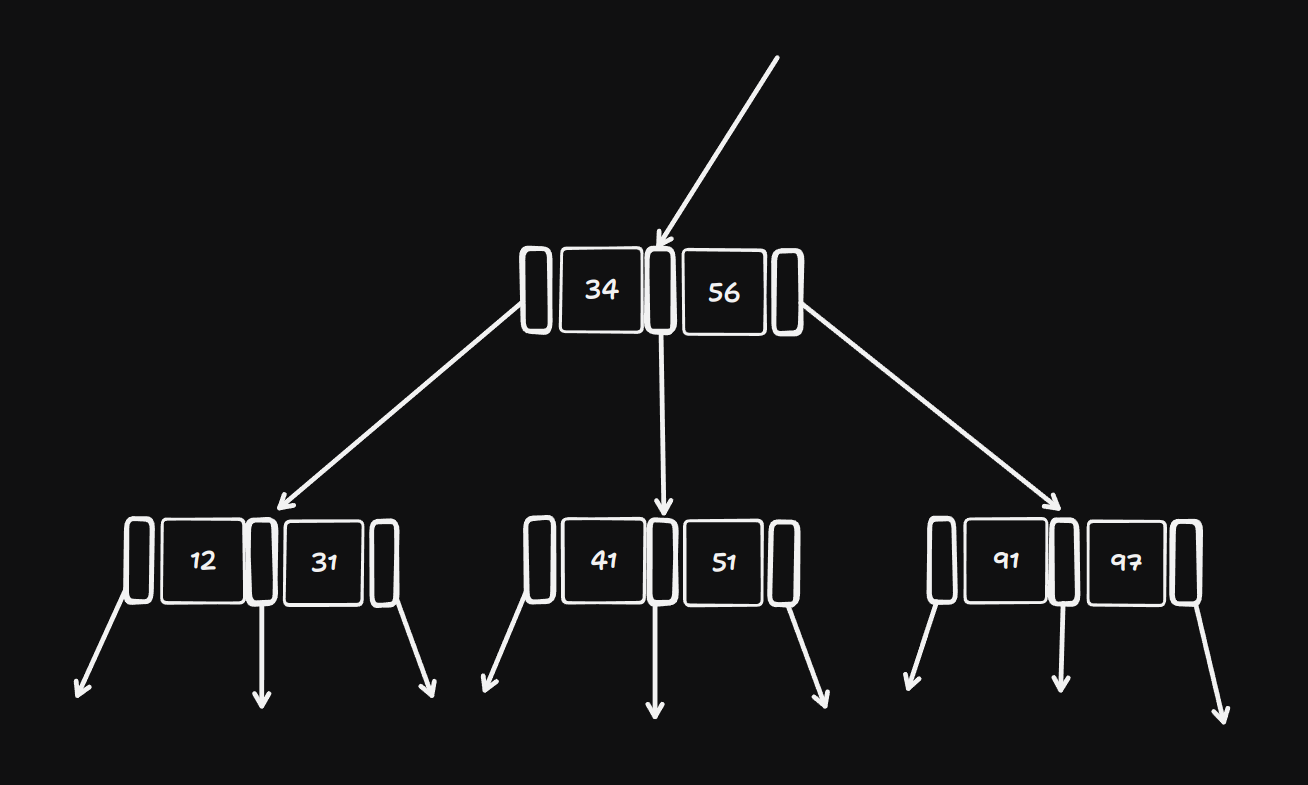
Balancing a B-Tree: with BST random insertions can leave a tree unbalanced which in turn makes it harder to find a key (at least the worst-case scenario), B-Trees the longest path is 𝑙𝑜𝑔𝑑𝑛, now with this, you will never visit more then 1+𝑙𝑜𝑔𝑑𝑛 nodes
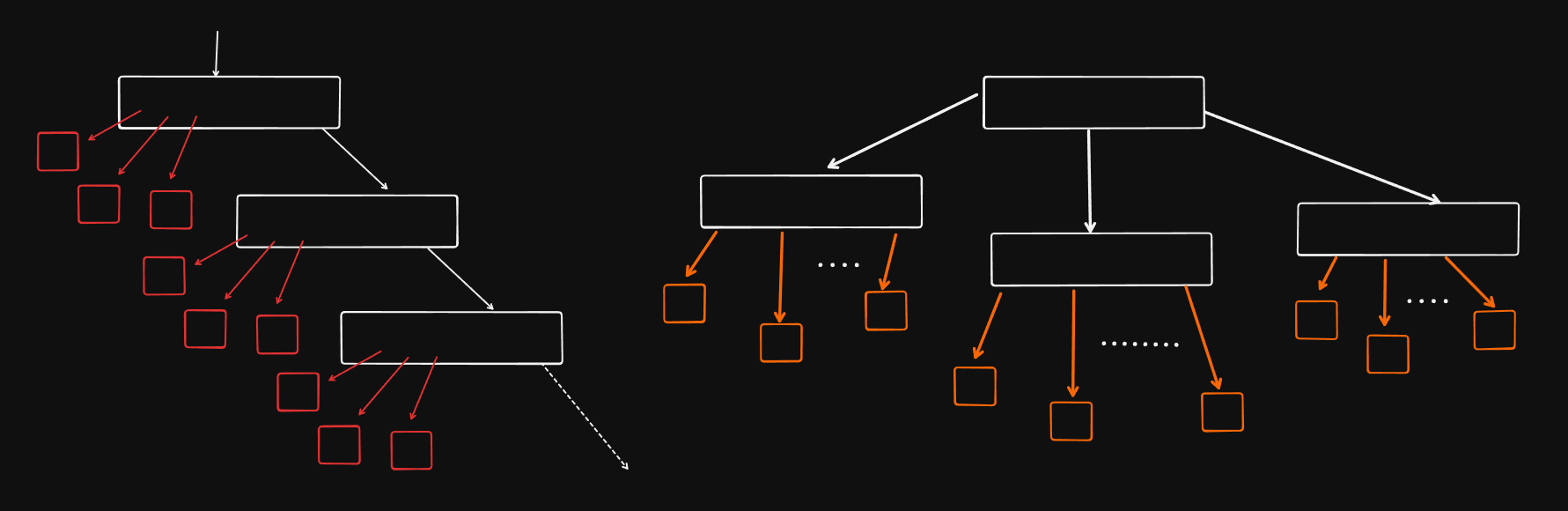
Insertion: First, a find proceeds from the root to locate the proper leaf for insertion. Then the insertion is performed, and balance is restored by a procedure which moves from the leaf back toward the root.
Deletion: Deletion in a B-tree also requires a find operation to locate the proper node. There are then two possibilities -
1. the key to be deleted resides in a leaf, or
2. the key resides in a nonleaf node. A non-leaf deletion requires that an adjacent key be found and swapped into the vacated position so that it finds work correctly
Now with these, there is a notion of underflow in the leaves as a minimum of 𝑑 keys is required so in order to restore the balance a key is borrowed from its neighbour, and if there aren't enough keys to distribute a concatenate happens to restore the balance.
B+ Trees
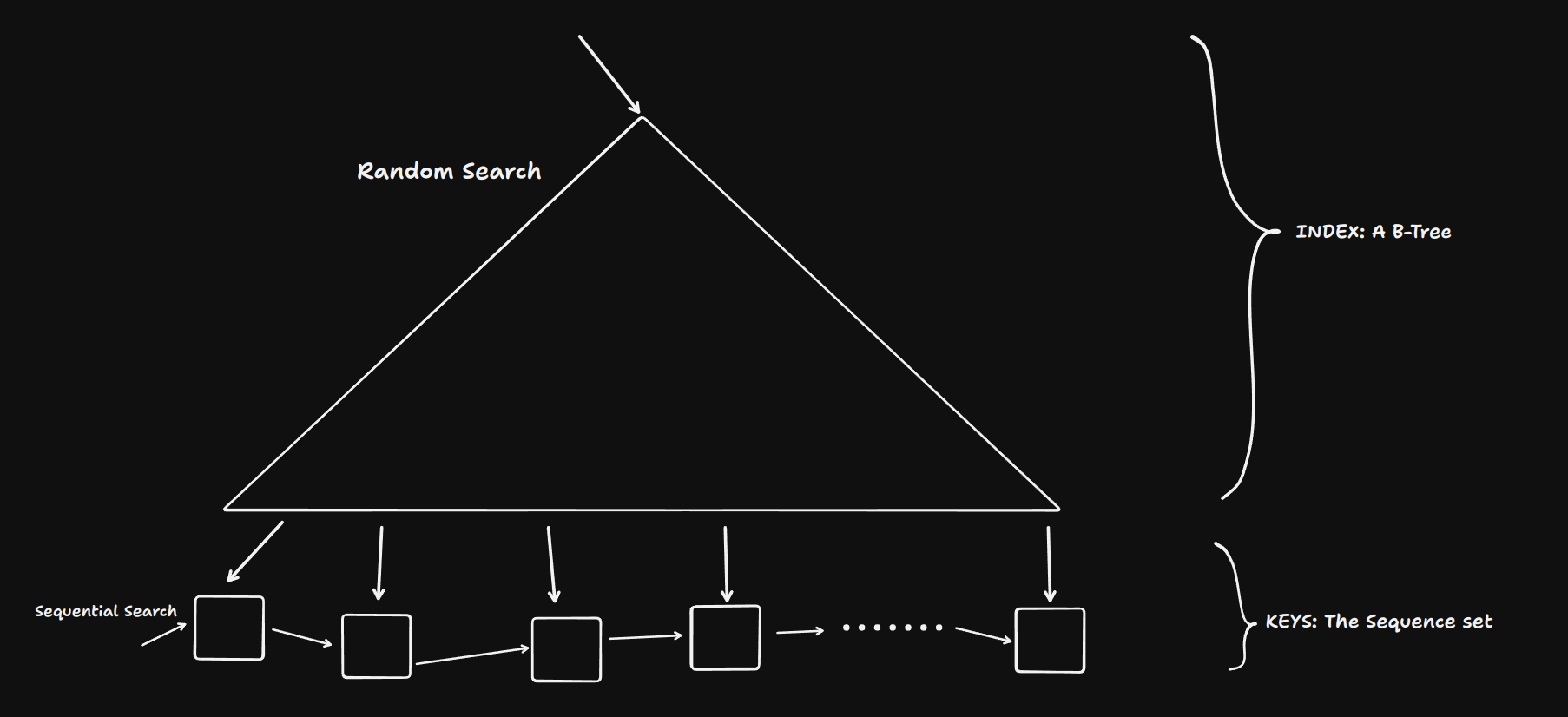
B+ Trees are a sophisticated evolution of the B-Tree, optimized for efficient range queries and disk-based storage systems. The key distinction lies in the separation of routing and data:
Leaf Nodes: Contain all key-value pairs in sorted order.
Non-Leaf Nodes: Serve as an index structure, containing only routing information.
Non-Leaf Node (𝑥)
𝑥.𝑛 : Number of router values
𝑥.𝑟𝑜𝑢𝑡𝑒𝑟[1..𝑛] : Sorted router values
(𝑥.𝑟𝑜𝑢𝑡𝑒𝑟[𝑖]<𝑥.𝑟𝑜𝑢𝑡𝑒𝑟[𝑖+1])
𝑥.𝑙𝑒𝑎𝑓 : Boolean flag set to
𝐹𝐴𝐿𝑆𝐸
𝑥.𝑐[1..𝑛+1] : Pointers to child nodes
Leaf Node (𝑥):
𝑥.𝑛 : Number of key-value pairs
𝑥.𝑘𝑒𝑦[1..𝑛] : Sorted key values
(𝑥.𝑘𝑒𝑦[𝑖]<𝑥.𝑘𝑒𝑦[𝑖+1])
𝑥.𝑙𝑒𝑎𝑓 : Boolean flag set to
𝑇𝑅𝑈𝐸
𝑥.𝑛𝑒𝑥𝑡 : Pointer to the next leaf node (for range queries)
![**Non-Leaf Node (𝑥)** - 𝑥.𝑛 : Number of router values - 𝑥.𝑟𝑜𝑢𝑡𝑒𝑟[1..𝑛] : Sorted router values (𝑥.𝑟𝑜𝑢𝑡𝑒𝑟[𝑖]<𝑥.𝑟𝑜𝑢𝑡𝑒𝑟[𝑖+1]) - 𝑥.𝑙𝑒𝑎𝑓 : Boolean flag set to 𝐹𝐴𝐿𝑆𝐸 - 𝑥.𝑐[1..𝑛+1] : Pointers to child nodes **Leaf Node (𝑥):** - 𝑥.𝑛 : Number of key-value pairs - 𝑥.𝑘𝑒𝑦[1..𝑛] : Sorted key values (𝑥.𝑘𝑒𝑦[𝑖]<𝑥.𝑘𝑒𝑦[𝑖+1]) - 𝑥.𝑙𝑒𝑎𝑓 : Boolean flag set to 𝑇𝑅𝑈𝐸 - 𝑥.𝑛𝑒𝑥𝑡 : Pointer to the next leaf node (for range queries)](https://cdn2.stablediffusionapi.com/attachements/84786b11-cb44-4879-9443-700a1507e57e.png)
A B+ Tree with sequential pages [Doubly Linked List] at its leaf level, some papers do link the non-leaf nodes as well so that is being shown using dotted connections
Critical Properties:

The search algorithm traverses from root to leaf, similar to B-Trees, with the key distinction that it always terminates at a leaf node. This property ensures consistent search time complexity.
Insertion
Locate target leaf node y via the search algorithm.
If y has available space, insert key k and terminate.
If y is full:
Allocate new node z.
Distribute keys:
First the keys remain in y.
Last t keys transfer to z.
Insert k into the appropriate node (y or z).
Update parent node x:
Insert pointer to z and new router value (typically last key in y).
If x lacks space, recursively split upwards.
Notably, B+ Trees propagate splits upward, potentially growing the root, in contrast to downward growth in some other structures.
Deletion
Locate and remove the key from the leaf node.
If underflow occurs:
Attempt redistribution with sibling nodes.
If redistribution fails, merge with a sibling.
Update parent routing information.
Propagate changes upward if necessary.
Key Observation:
Deletion only modifies leaf nodes and updates routing information in non-leaf nodes, never removing entries from the latter.
The B+ Tree's structure makes it particularly well-suited for systems requiring efficient range queries and where data primarily resides on disk or other high-latency storage media. Its ability to maintain a shallow, wide structure allows for minimized I/O operations in large datasets, a critical factor in database and file system performance.
Optimizing insertions for B+ Trees
Now optimizations are where we do have to remember the hierarchical structure of the memory
Standard B+ Tree implementations, while theoretically elegant, often suffer from severe performance degradation when faced with real-world, high-throughput scenarios. Let's dissect the primary bottlenecks:
Root-to-leaf Traversal Overhead: Each random insertion necessitates a complete traversal from root to leaf. In large-scale systems, this results in I/O operations per insertion, which becomes prohibitively expensive as grows.
𝑂(𝑙𝑜𝑔𝑛)𝑛
Cache-Unfriendly Random Page Modifications: The stochastic nature of insertions leads to unpredictable page modifications across the tree structure. This behaviour is anathema to modern CPU cache architectures, resulting in frequent cache misses and suboptimal memory access patterns.
Underutilized Leaf Nodes: Typical B+ Tree implementations maintain leaves at approximately 50% capacity to facilitate splits and merges. While this simplifies rebalancing operations, it leads to significant wasted space and increased tree depth.
The root cause of these inefficiencies lies in the use of
randomly distributed key indices
. While beneficial for even distribution, this randomness wreaks havoc on the locality of reference and predictable access patterns.
Leveraging Sorted Insertions for Optimized Performance :
Localized Page Access: By maintaining insertions on the rightmost path of the tree, we dramatically improve cache utilization. This approach allows for prefetching and reduces TLB misses and we can ignore the leftmost part of the tree at least when it comes to Insertions.
Controlled Fill Factor: Sorted insertions enable precise control over leaf node utilization. By maintaining a higher fill factor (e.g., 80-90%), we can significantly reduce the overall tree depth and improve space efficiency. Typically in large systems, B+ Trees are 2/3rd's of the way full.
Sequential Disk Layout: Sorted keys naturally lead to a more contiguous on-disk representation of leaf nodes. This alignment with underlying storage characteristics can yield substantial I/O performance gains, especially on HDDs or SMR drives.
UUIDv7: Uniqueness and Sortability
The advent of UUIDv7 provides an elegant solution to the seemingly contradictory requirements of unique identifiers and sortable keys. By encoding a high-precision timestamp in the most significant bits, UUIDv7 offers:
Temporal Sorting: Keys are naturally ordered by creation time, facilitating the sorted insertion optimizations discussed above.
Maintained Uniqueness: The inclusion of random bits ensures collision resistance even in high-concurrency environments.
Distributed Generation: UUIDs can be generated without coordination, crucial for distributed systems.
Empirical Observations and Hypotheses
While the exact implementations of large-scale object storage systems like AWS S3 or Cloudflare R2 are not public, observed behaviour suggests potential B+ Tree-like underpinnings. Specifically, the correlation between bucket size and post-handshake upload latency hints at tree rebalancing operations as a potential bottleneck.
Given that a production-grade B+ Tree with a depth of 2 can easily accommodate around 10 billion entries, the optimizations proposed here could yield significant benefits:
Reduced Rebalancing Frequency: Sorted insertions naturally lead to fewer tree restructuring operations.
Improved Cache Efficiency: By localizing insertions to a specific region of the tree, we can maintain critical pages in the cache for extended periods.
Enhanced I/O Patterns: The more predictable nature of insertions allows for more effective I/O scheduling and potential write coalescing.
Conclusion and Future Directions
While these optimizations offer substantial improvements, they are not a panacea for all storage system designs. The efficacy of these approaches depends heavily on workload characteristics and system requirements. Future research directions might include:
Adaptive algorithms that dynamically adjust between random and sorted insertion strategies based on observed workload patterns.
Integration with emerging storage technologies like ZNS SSDs to further optimize physical data layout. (most likely they use zoned drives)
Exploration of hybrid data structures that combine the strengths of B+ Trees with other indexing mechanisms for specific use cases.
As we continue to push the boundaries of large-scale data management, such optimizations will become increasingly crucial. The intersection of data structure design, systems architecture, and hardware characteristics remains a fertile ground for innovation in the pursuit of performant and scalable storage solutions.
